主成分分析を使ってバウンティボックスを作る
以前にnumpyを使った主成分分析を公開しましたが、今回はそれを使ってバウンティボックスを作ってみます。
ある頂点集合に対して、適切なバウンティボックスを求めたいとしましょう。簡単に思いつく方法としては、基底軸X,Yごとに最大値&最小値を求め、それらの頂点を囲む方法です。
しかし、その方法では最適なバウンティボックスにならない場合があります(下左図参照)、頂点集合に対して適切な基底軸を求めれば最適に「近い」バウンティボックスを得ることができます。
主成分分析(principal component analysis)
適切な基底軸を求めるために登場するのが「主成分分析」です。
これはもともと統計学や経済学で発明された分析手法で、似たものに「因子分析」がありますが、これはまたの機会に・・・
主成分分析は特に難しい話ではありません、高校数学レベルの知識があれば十分理解可能です。
まず頂点集合を行列と見なし各列要素から平均値を差し引きます、それを「共分散行列」と呼びます。
その共分散行列の「固有ベクトル」を求めれば良いのです。
#coding:utf-8 import numpy def PCA(P): """主成分分析""" m = sum(P) / float(len(P)) P_m = P - m l,v = numpy.linalg.eig( numpy.dot(P_m.T,P_m) ) return v
固有値・固有ベクトルとは、ある行列に対して向きが変わらないベクトルを「固有ベクトル」、そのベクトルの取りうる長さを「固有値」と言います。
このケースで言えば、行列要素の分散(ばらつき)が最小となる基底ベクトルを求めていると考えてください。
実際にやってみよう
まず、ランダムに偏った頂点群を生成します。
N = 20 t = numpy.random.rand(N) x = t+numpy.random.rand(N)*0.3 y = t+numpy.random.rand(N)*0.3
生成した頂点群を主成分分析します。
pca = PCA(numpy.array(zip(x,y)))
主成分分析の答えとして、分散が最小となり基底ベクトルが返ってきます。
「基底ベクトルを並べた行列」=「基底座標系への回転行列」ですので、頂点群を主成分座標系に変換し、軸ごとの最大値、最小値を求めます。
v = [] mx = numpy.mean(x) my = numpy.mean(y) for tx,ty in zip(x,y): ax,ay = numpy.dot(pca,[(tx-mx),(ty-my)]) v.append( dict(ax=ax,ay=ay,x=tx,y=ty) ) maxx = max(v,key=lambda x:x['ax']) minx = min(v,key=lambda x:x['ax']) maxy = max(v,key=lambda x:x['ay']) miny = min(v,key=lambda x:x['ay'])
各軸ごとの最大値/最小値が求まりましたね。
2次元の場合は4つ、3次元の場合は6つの最大値/最小値を求まります、ここで欲しい情報は「平面の方程式」となりますので、各要素を以下のように求めます。
- 平面上の任意の点=最大値/最小値
- 法線ベクトル=基底軸と直交した基底ベクトル
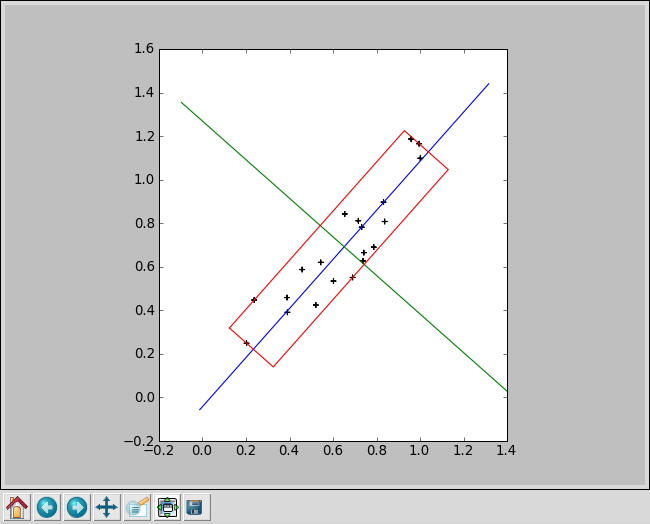
今回は2次元のバウンティボックスを、「matplotlib」を使ってグラフ化してみます。
def cross_point(x1,y1,x2,y2,x3,y3,x4,y4): """2直線の交点を求める""" den = (y4-y3)*(x2-x1)-(x4-x3)*(y2-y1) if den == 0: return None return ((x4-x3)*(y1-y3)-(y4-y3)*(x1-x3))/den #グラフ描画 from pylab import * a = subplot(111, aspect='equal') a.scatter(x, y, marker="+") #点描画 #基底ベクトルの描画 v1x,v1y = pca[1] a.plot([mx+v1x,mx-v1x],[my+v1y,my-v1y]) v2x,v2y = pca[0] a.plot([mx+v2x,mx-v2x],[my+v2y,my-v2y]) #点集合を囲む四角形を描画 boxx=[] boxy=[] t1 = cross_point(maxx['x'],maxx['y'], maxx['x']+v1x,maxx['y']+v1y, maxy['x'],maxy['y'], maxy['x']+v2x,maxy['y']+v2y) t2 = cross_point(maxx['x'],maxx['y'], maxx['x']+v1x,maxx['y']+v1y, miny['x'],miny['y'], miny['x']+v2x,miny['y']+v2y) t3 = cross_point(minx['x'],minx['y'], minx['x']+v1x,minx['y']+v1y, miny['x'],miny['y'], miny['x']+v2x,miny['y']+v2y) t4 = cross_point(minx['x'],minx['y'], minx['x']+v1x,minx['y']+v1y, maxy['x'],maxy['y'], maxy['x']+v2x,maxy['y']+v2y) boxx.append(maxx['x']+t1*v1x) boxy.append(maxx['y']+t1*v1y) boxx.append(maxx['x']+t2*v1x) boxy.append(maxx['y']+t2*v1y) boxx.append(minx['x']+t3*v1x) boxy.append(minx['y']+t3*v1y) boxx.append(minx['x']+t4*v1x) boxy.append(minx['y']+t4*v1y) boxx.append(boxx[0]) boxy.append(boxy[0]) a.plot(boxx,boxy) show()